Hi,
I have some difficulties to understand the answer of one of the practice problem of the reading relating to Non-current liabilities. The question is the 12: "For a bond issued at a premium, using the effective interest rate method, the: A ) carrying amount increases each year.
B ) amortization of the premium increases each year.
C ) premium is evenly amortized over the life of the bond. »
the answer A is definitely wrong because the carrying value should decrease every year since the bond was issued at a premium
the answer C refers to a straight line amortization
The answer B is the correct answer according to the book but in my opinion it is wrong too because since the carrying value decreases every year, the interest expense (effective interest rate x carrying value) should decrease every year too and the premium amortization which is the difference between this interest expense and the interest paid (which is fixed) should therefore decrease every year too?
Could someone explain me why I am wrong or what I missed?
Thanks in advance!
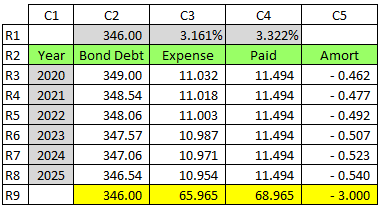
I suggest that you set up an amortization table in Excel to see why B is correct.
Try a 10-year, annual-pay, 6% coupon, $1,000 par bond issued at $1,100.
Here’s the mathematical intuition behind WHY the amortization is greater each year.
A market rate bond (i.e. where coupon - YTM) will trade at par. So, if coupon is > YTM, the bond trades at a premium. And the premium will be the PV of the “additional” (i.e. relative to a market rate bond) coupon payments. So, if you had a 10% YTM and an 11% coupon on a 30-year bond, the 11% bond would provide $10 more per year than the 10% bond (assuming a $1,000 par value)for 30 years. And the premium would be the PV of those payments at a 10% discount rate (in other words, the bond would sell for $1,094.27, and the PV of a 30-period $10 annuity at 10% is $94.27).
The premium in the next period would be the PV of a 29 period, $10 annuity, or $93.70.
The difference between the two (i.e. the amortization of the premium in the first year) is the PV of that 30th payment. Check that out for yourself - what’s the PV of $10 at 15% for 30 years?
The next period, the premium will now be the PV of a 28 period annuity, or $93.07. So, the first year, the premium went down by $0.57, and the second by $0.63. Each year, the Premium goes down by the PV of the “last” payment. And since the annuity gets shorter each year, the PV of that last payment gets larger.
Hi S2000magician, Busprof,
Thanks a lot for answering.
After starting to do all the computation by myself on paper I realized how stupid my question was… Thanks again for helping and for the explanations!
Even simpler:
Coupon > Market Rate
so
Bond Price > Par
Interest Paid = Par x Coupon (fixed throughout)
Interest Expense = Bond Price/Carrying Value x Market Rate (decreases towards maturity)
Interest Paid > Interest Expense
Interest Paid — Interest Expense = Amort of Premium
Since Interest Paid is fixed throughout and Interest Expense decreases towards maturity therefore Amort of Premium increases.
Sample table: