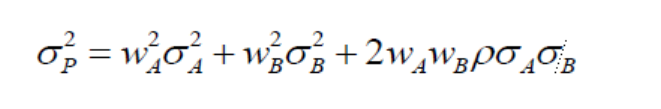From Kaplan:
For a portfolio of traditional securities, adding alternative investments such as hedge funds can potentially increase the portfolio’s expected returns, because these investments often have higher expected returns than traditional investments, and decrease portfolio variance, because returns on these investments are less than perfectly correlated with returns on traditional investments.
My assumption was hedge fund returns would vary more, not less from the S&P’s returns. Wouldn’t that increase variance?
How about the correlation of alternative investments with traditional investments? 
Hmm. “because returns on these investments are less than perfectly correlated with returns on traditional investments.”
…A perfect correlation would be either 1 or -1…
So the correlation of alternative investments with traditional investments aren’t perfectly correlated.
So if they aren’t perfectly correlated, wouldn’t that increase the variance of returns?
When they say “perfectly correlated” they mean a correlation of +1 only.
They also mean a correlation of returns (as opposed to a correlation of prices).
Finance people are incredibly sloppy in the language they use; this often leads to similarly sloppy thinking.
So to be perfectly correlated (+1), the traditional investment’s return would have to be the same as the alternative investment’s return?
No.
For example, these two sequences of returns have a correlation of +1:
- 0%, 1%, 0%, 1%, 0%, 1%
- 0%, 2%, 0%, 2%, 0%, 2%
So do these:
- 1%, 2%, 1%, 2%, 1%, 2%
- −2%, −1%, −2%, −1%, −2%, −1%
Are you making the point that any two selected returns can be perfectly correlated?
No.
I’m making the point that correlation takes into account differences in average returns, and differences in volatilities of returns.
Most finance people don’t understand correlation (and, therefore, frequently reach stupid conclusions about it).
This is the variance equation for a two asset portfolio. However, the concept remains the same, because a portfolio can also be considered an asset “as a whole.”
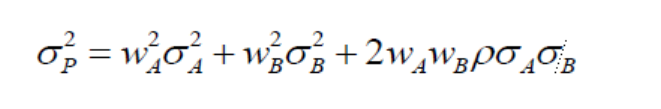
Assume:
STD of Asset A, Hedge Fund Portfolio.
STD of Asset B, Traditional Portfolio.
Assume equal weightings (50% in each) between the portfolios Wa = Wb = 0.5.
Focus on this term.
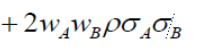
@ p = 0. No correlation. This whole term goes to zero. Reducing the total variance as this term is eliminated in the equation because anything x 0 is zero.
@ p = 1. Perfect positive correlation. This term would remain, but at its largest, maximizing variance.
@ 0 < p < 1. The whole term will remain but smaller with a total variance less than when p = 1. The answer to your question.
@ -1 < p < 0. You start seeing “hedging” effects, where the term still exists but has a variance “reducing” effect, because that whole term will now be negative.
Substitute numbers to see this effect.
Correlation only implies a relationship between the two.
It does not suggest there will be similar returns.
The approximate return can not be inferred, unless you derive an accurate, properly specified linear or multiple regression model from that return data, which is simply a line (or plane, cube, etc.) of best fit.
For the example S2000 provided:
X: 1, 2, 1, 2, 1, 2
Y: −2, −1, −2, −1, −2, −1
From linear regression, produces:
Y = -3+1X
This equation correctly determines the returns for the Y series for each value of the X series.
Correlation was required in order to determine this equation (a longer explanation).
But from correlation alone, you can not determine the approximate return (Y).
These are good explanations that I will come back to for a reference.