Dear All- Given below is a question from schweser. Kindly help Two samples were drawn from two normally distributed populations. For the first sample, the mean was $50 and the standard deviation was $5. For the second sample, the mean was $55 and the standard deviation was $6. The first sample consists of 25 observations and the second sample consists of36 observations. My question is which test statistic (Either t or z) should be used to analyse sample one and sample two (Please give reasons also)
Because the first sample is small (less than 30), use a t-statistic.
Because the second sample is large (30 or greater), you can use a z-statistic, though a t-statistic is acceptable (but a little more conservative).
Dear Magician- In schweser one table of rules for selecting tests is given. according to it if population variance is unknown t statistic should be used. for large populations also the t statistic can be used though it is conservative. Your answer is in agreement with that but reason you gave is “sample size small”. What is the real reason 1) smallness of sample or 2) not knowing variance.
I am slightly confused, please guide.
One more point - according to rules of schweser, if population variance is know z test can be used irrespective of size of sample.
You should not use the Z-statistic for a dataset with an unknown population variance. It might be acceptable if the sample size is large enough, but as S2k said, it’s more conservative to use the t-distribution.
Use t for the first, and z for the second.
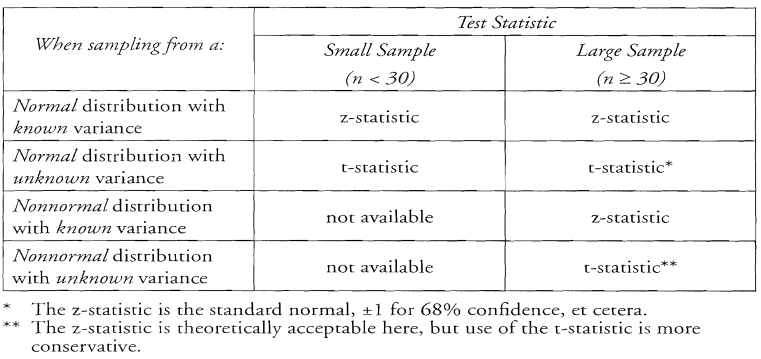
Z-test cannot always be used irrespective of sample size. For instance, in the case of a small sample from a non-normal distribution we cannot use a t or a z-test.
The matter of small vs large sample brings in to play the Central Limit Theorem. When a sample size is small, the sampling distribution of x-bar is not necessarily normally distributed. Therefore, in a small sample, we must have a normal distribution for the population in order for any tests to be valid.
If we have a sufficiently large sample (convention and research shows around 30 and higher), the sampling distribution of x-bar will be normally distributed. In this case, we don’t need to have a normally distributed population, because the sampling distribution of x-bar will be normally distributed.
The t-distribtuion actually depends on the degrees of freedom, and this distribution converges to the z distribution as the sample size increases.
So, we can see that with a large enough sample, the CLT allows us to use a z-distribution, and the t-distributiion will converge to this z-distribution as n increases. With a small sample, we can’t rely on the central limit theorem, and need a more conservative distribution that accounts for the degrees of freedom in our sample-- so a t-distribution comes in to use, so long as we know (assume in most cases) the population is normally distributed.
Thanks a lot guys. This has cleared my doubts.
Good to hear.